Mô hình FEM là gì? Lưu ngay 5 bước tính toán FEM dân kỹ thuật phải biết

Trong lĩnh vực kỹ thuật và kỹ thuật cơ khí, mô hình FEM đã trở thành một công cụ quan trọng. Nó không chỉ giúp mô phỏng mà còn dự đoán và hiểu biết hành vi của các hệ thống phức tạp. Đối diện với các thách thức của cấu trúc, vật liệu và thiết kế, FEM trở thành trợ thủ đắc lực cho các kỹ sư và nhà nghiên cứu. 

Hãy cùng tìm hiểu về cơ bản của mô hình FEM là gì? Và lưu ngay 5 bước tính toán mà dân kỹ thuật nên biết để áp dụng mô hình FEM một cách hiệu quả.

Mô hình FEM là gì?

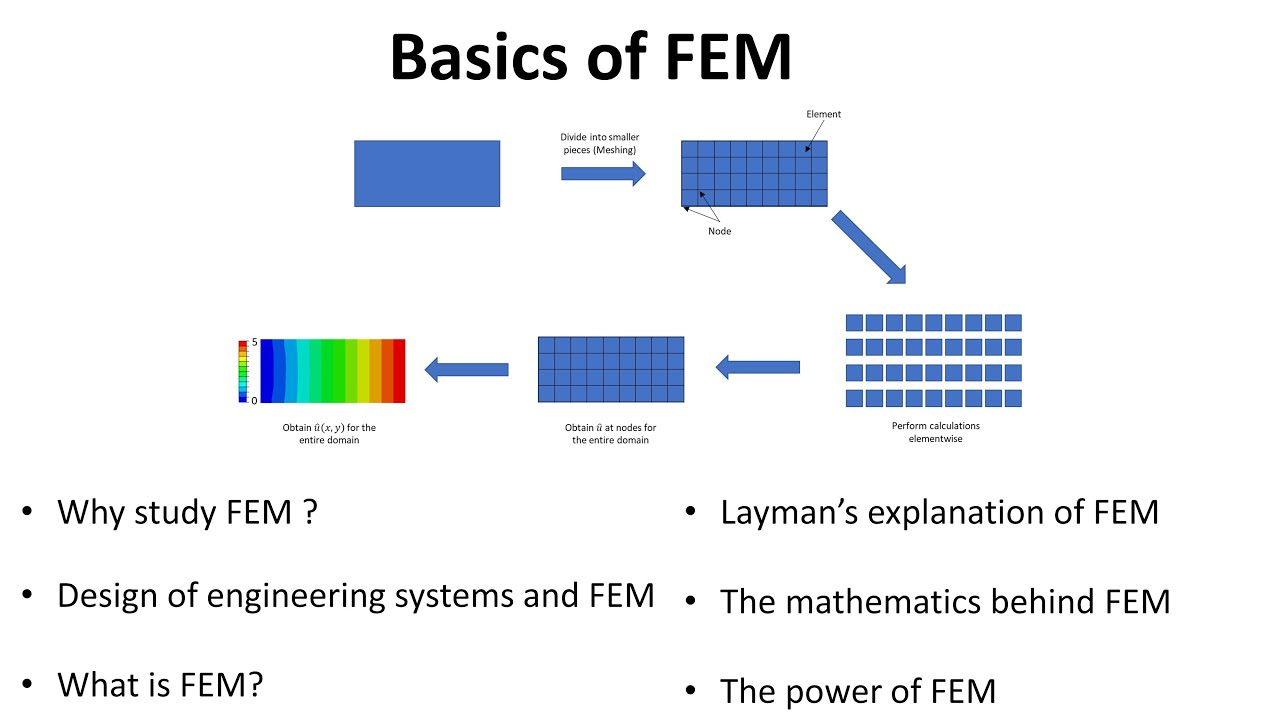
FEM có thể là viết tắt của Finite Element Method (phương pháp phần tử hữu hạn). Đây là một phương pháp trong lĩnh vực kỹ thuật cơ học để giải các vấn đề phức tạp bằng cách chia chúng thành các phần tử nhỏ hơn để dễ quản lý tính toán.

Mô hình FEM (Finite Element Model) là một phương pháp trong lĩnh vực kỹ thuật cơ học để mô phỏng và giải quyết các vấn đề phức tạp của cấu trúc và vật liệu. FEM giúp chuyển đổi một hệ thống liên tục và phức tạp thành một hệ thống các phần tử nhỏ, dễ quản lý, và giải quyết các phương trình toán học để mô phỏng và dự đoán hành vi của hệ thống.

Một số khái niệm liên quan đến FEM

FEM được sử dụng rộng rãi trong ngành kỹ thuật để mô phỏng và giải quyết các vấn đề liên quan đến cơ học, nhiệt độ, và động học của các hệ thống phức tạp. Dưới đây là một số khái niệm cơ bản về FEM:

1. Phần Tử (Element): Là một đơn vị nhỏ, đơn giản và hình học có thể được mô tả bằng phương trình toán học. Các phần tử được sắp xếp để tạo thành mô hình FEM.

2. Nút (Node): Là các điểm trong không gian mà các đoạn thẳng giữa chúng mô tả biên của các phần tử. Nút thường chứa các giá trị không gian (ví dụ: tọa độ XYZ) và các giá trị nghiệm cần được xác định.

3. Biến Cố (Elemental Equation): Là một hệ phương trình toán học mô tả mối quan hệ giữa các nút của mỗi phần tử. Các biến cố giúp mô tả hành vi của phần tử trong hệ thống tổng thể.

4. Ma Trận Độ Cứng (Stiffness Matrix): Là một ma trận thể hiện sức đàn hồi của các phần tử trong mô hình. Ma trận này liên quan đến các thuộc tính cơ học của vật liệu và hình học của phần tử.

5. Điều Kiện Ran (Boundary Conditions): Là các điều kiện mà giá trị của biến cố hoặc nút đã biết trước, và không thay đổi trong quá trình giải phương trình.

6. Hệ Thống Phương Trình Cân Bằng (System of Equations): Là hệ phương trình tuyến tính được tạo ra từ việc kết hợp các biến cố của tất cả các phần tử trong mô hình. Giải hệ phương trình này sẽ cung cấp giá trị của các biến cố chưa biết.

7. Hệ Số Tăng Cường (Enrichment Factor): Là một yếu tố đánh giá độ chính xác của mô hình FEM. Các phương pháp tăng cường thường được sử dụng để cải thiện kết quả trong các vùng quan trọng.

Những khái niệm cơ bản trên giúp hiểu rõ hơn về cách FEM hoạt động và cách nó được áp dụng để mô phỏng các vấn đề kỹ thuật và khoa học.

Vai trò của FEM

FEM là một công cụ mạnh mẽ trong lĩnh vực xử lý dữ liệu địa lý và chuyển đổi dữ liệu giữa các định dạng khác nhau. Nó được ứng dụng trong nhiều lĩnh vực, giúp: 

• Chuyển đổi dữ liệu địa lý: FEM cho phép chuyển đổi dữ liệu địa lý giữa các định dạng và hệ thống tham chiếu không gian khác nhau, như từ ESRI Shapefile sang GeoJSON hoặc từ WGS84 sang UTM.

• Tích hợp dữ liệu: FEM có thể tích hợp dữ liệu từ nhiều nguồn khác nhau. Bao gồm cả cơ sở dữ liệu, tệp văn bản, dữ liệu địa lý, và nhiều nguồn dữ liệu khác.

• Xử lý dữ liệu lớn: FEM được thiết kế để xử lý dữ liệu lớn và phức tạp. Điều này làm cho nó trở thành một công cụ hiệu quả khi làm việc với các tập dữ liệu địa lý có kích thước lớn.

• Tạo và xử lý dữ liệu 3D: FEM hỗ trợ tạo và xử lý dữ liệu 3D, giúp các chuyên gia GIS và địa lý tạo ra và làm việc với mô hình không gian ba chiều.

• Tích hợp trong quy trình làm việc tự động: FEM có thể tích hợp trong các quy trình làm việc tự động (workflow) để tự động hóa các nhiệm vụ chuyển đổi và xử lý dữ liệu.

• Quản lý dữ liệu doanh nghiệp: Các tổ chức có thể sử dụng FEM để quản lý và duyệt qua các nguồn dữ liệu doanh nghiệp một cách hiệu quả, đồng bộ hóa thông tin giữa các hệ thống.

• Phân tích địa lý và báo cáo: FEM hỗ trợ thực hiện các phân tích địa lý và tạo báo cáo dựa trên dữ liệu địa lý được chuyển đổi và tích hợp.

FEM cung cấp API (Application Programming Interface) và các trình kịch bản (scripting) để tích hợp và tùy chỉnh quá trình xử lý dữ liệu. Những ứng dụng trên giúp FEM trở thành một công cụ đa nhiệm và linh hoạt trong việc quản lý, chuyển đổi. Có thể tích hợp dữ liệu địa lý cho nhiều ứng dụng khác nhau.

Ứng dụng FEM vào đâu?

FEM đã được áp dụng rộng rãi trong nhiều lĩnh vực khác nhau. Dưới đây là một số ứng dụng phổ biến của FEM:

• Cơ Học Kết Cấu: FEM được sử dụng để phân tích và thiết kế cấu trúc kết cấu như cầu, tòa nhà, cột, và các thành phần cơ học khác để đảm bảo tính chất cơ học và an toàn.

• Ô Tô và Hàng Không: Trong ngành ô tô và hàng không, FEM được sử dụng để mô phỏng và phân tích các thành phần cơ học, động lực, và độ an toàn của các bộ phận của xe và máy bay.

• Chế Tạo và Kỹ Thuật Máy: FEM được áp dụng trong quá trình thiết kế và phân tích các bộ phận máy, máy móc, và thiết bị chế tạo để đảm bảo chúng đáp ứng các yêu cầu về cơ học và độ bền.

• Năng Lượng và Môi Trường: Trong lĩnh vực năng lượng và môi trường, FEM được sử dụng để phân tích và tối ưu hóa thiết bị như turbine gió, ống dẫn nước, và các cấu trúc liên quan đến nguồn năng lượng tái tạo.

• Y Học và Thiết Bị Y Tế: Trong lĩnh vực y học, FEM có thể được sử dụng để mô phỏng và phân tích cơ học của các bộ phận cơ thể, thiết bị y tế, và cả quá trình truyền nhiệt trong cơ thể.

• Các ứng dụng Cảm Biến và Thiết Bị Điện Tử: FEM có thể được sử dụng để mô phỏng và phân tích cơ học của các cảm biến và thiết bị điện tử, đảm bảo chúng đáp ứng các yêu cầu độ bền và độ chính xác.

• Dầu Khí và Khai Thác Tài Nguyên: Trong ngành dầu khí, FEM được sử dụng để phân tích và thiết kế các cấu trúc liên quan đến khoan dầu, ống dẫn, và hệ thống liên quan.

• Các ứng dụng Điện Tử và Điện Tử Tiêu Dùng: FEM có thể được áp dụng trong thiết kế và phân tích các sản phẩm điện tử, từ điện thoại thông minh đến các thiết bị tiêu dùng khác.

FEM là một công cụ mạnh mẽ giúp các kỹ sư và nhà nghiên cứu nắm bắt và hiểu biết về hành vi cơ học và nhiệt độ của các hệ thống phức tạp, đồng thời giúp tối ưu hóa thiết kế và đảm bảo hiệu suất và an toàn.

5 bước tính toán FEM dân kỹ thuật phải biết

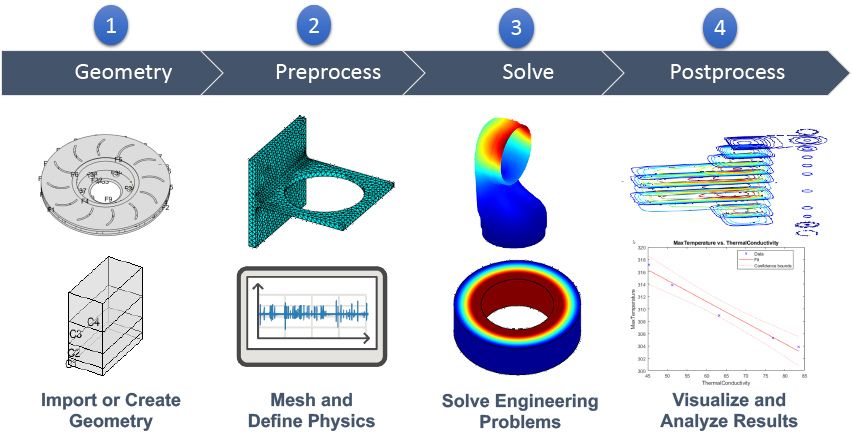
Quá trình tính toán FEM (Finite Element Method) đòi hỏi sự hiểu biết vững về cả lý thuyết và phương pháp thực hành. Dưới đây là 5 bước quan trọng mà dân kỹ thuật thường phải biết khi thực hiện tính toán FEM:

1. Chia đối tượng thành phần tử (Element): Bước đầu tiên là chia đối tượng cần mô phỏng thành các phần tử hữu hạn. Chẳng hạn như tam giác hoặc tứ giác trong không gian 2D, hoặc các khối, cầu, hình chóp trong không gian 3D.

2. Xác định các thông số vật lý và điều kiện biên (Material Properties and Boundary Conditions): Xác định các thông số vật lý của vật liệu được sử dụng trong mô phỏng, như độ cứng, độ co giãn, hoặc đặc tính nhiệt độ. Đồng thời, đặt các điều kiện biên như áp suất, lực tác động, và nhiệt độ môi trường.

3. Xác định các hệ số phân bố: Xác định các hệ số phân bố áp dụng lên các phần tử FEM.

4. Giải hệ thống phương trình (Solve the System of Equations): Sử dụng các phương pháp số học và thuật toán giải hệ thống phương trình tuyến tính để tìm ra giá trị của biến cố chưa biết. Các giải thuật như Gauss-Seidel, Jacobi, hoặc phương pháp lặp chéo (iterative methods) thường được sử dụng.pháp số học và thuật toán giải hệ thống phương trình tuyến tính để tìm ra giá trị của biến cố chưa biết. 

5. Tính toán kết quả: Tìm kết quả cuối cùng từ các giá trị tính toán được tại các điểm trong vật thể.

Lưu ý rằng quá trình này có thể được lặp lại và điều chỉnh để đảm bảo sự chính xác và tính ổn định của mô hình. Đồng thời, việc sử dụng phần mềm chuyên nghiệp như ANSYS, Abaqus, và COMSOL thường giúp tối ưu hóa quá trình tính toán FEM. 

Hy vọng đọc giả hiểu rõ FEM là gì? Cũng như tầm quan trọng của phương pháp tính toán FEM trong ngành kỹ thuật hiện nay. 

Theo dõi Vieclamnhamay.vn để biết thêm nhiều thông tin về chuyên ngành và tuyển dụng kỹ sư nhà máy nhé!

Ms. Công Nhân